Advertisements
Advertisements
Question
A cylindrical object of outer diameter 10 cm, height 20 cm and density 8000 kg/m3 is supported by a vertical spring and is half dipped in water as shown in figure. (a) Find the elongation of the spring in equilibrium condition. (b) If the object is slightly depressed and released, find the time period of resulting oscillations of the object. The spring constant = 500 N/m.
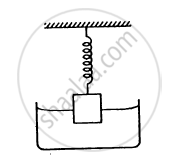
Solution
Given:
Diameter of the cylindrical object, d = 10 cm
∴ Radius, r = 5 cm
Height of the object, h = 20 cm
Density of the object, ρb = 8000 kg/m3 = 8 gm/cc
Density of water, ρw = 1000 kg/m3
Spring constant, k = 500 N/m = 500 × 103 dyn/cm
(a) Now,
F + U = mg [F = kx]
Here, U is the upward thrust and x is the small displacement from the equilibrium position.
kx + Vρwg = mg
\[\Rightarrow 500 \times {10}^3 \times (x) + \left( \pi r^2 \right) \times \left( \frac{h}{2} \right) \times 1 \times 1000 = \pi r^2 \times h \times \rho_b \times 1000\]
\[ \Rightarrow 500 \times {10}^3 \times (x) = \pi r^2 \times \text{h} \times 1000\left( \rho_b - \frac{1}{2} \right)\]
\[ = \pi \times (5 )^2 \times 20 \times 1000\left( \rho_b - \frac{1}{2} \right)\]
\[ \Rightarrow 50x = \pi \times 25 \times 2 \times \left( \rho_b - \frac{1}{2} \right)\]
\[x = \pi(8 - 0 . 5)\]
\[\text{or, x }= \pi \times 7 . 5 = 23 . 5 \text{ cm} \]
(b) We know that X is the displacement of the block from the equilibrium position.
Now,
Driving force : \[\text{F = kX + V }\rho_\text{w} \times \text{g}\]
\[ \Rightarrow\text{ ma = kx }+ \pi \text{r}^2 \times (\text{X}) \times \rho_\text{w} \times\text{ g}\]
\[ = (\text{k} + \pi \text{r}^2 \times \rho_\text{w} \times g)\text{x}\]
\[ \Rightarrow \omega^2 \times (X) = \frac{\left( k + \pi r^2 \times \rho_\text{w} \times g \right)}{\text{m}} \times (X)\]
\[\text{In SHM }\left( a = \omega^2 \text{X} \right), \text{ time period }\left( T \right) \text{is}\]
\[ T = 2\pi\frac{m}{k + \pi r^2 \times \rho_w \times g}\]
\[ =2\pi\frac{\pi \times 25 \times 20 \times 8}{500 + {10}^3 + \pi \times 25 \times 1 \times 1000}\]
= 0.935 s
APPEARS IN
RELATED QUESTIONS
Why is it easier to swim in sea water than in fresh water?
A ferry boat loaded with rocks has to pass under a bridge. The maximum height of the rocks is slightly more than the height of the bridge so that the boat just fails to pass under the bridge. Should some of the rocks be removed or some more rocks be added?
A 20 N metal block is suspended by a spring balance. A beaker containing some water is placed on a weighing machine which reads 40 N. The spring balance is now lowered so that the block gets immersed in the water. The spring balance now reads 16 N. The reading of the weighing machine will be
A metal cube is placed in an empty vessel. When water is filled in the vessel so that the cube is completely immersed in the water, the force on the bottom of the vessel in contact with the cube
A solid floats in a liquid in a partially dipped position.
(a) The solid exerts a force equal to its weight on the liquid.
(b) The liquid exerts a force of buoyancy on the solid which is equal to the weight of the solid.
(c) The weight of the displaced liquid equals the weight of the solid.
(d) The weight of the dipped part of the solid is equal to the weight of the displaced liquid.
A solid is completely immersed in a liquid. The force exerted by the liquid on the solid will
(a) increase if it is pushed deeper inside the liquid
(b) change if its orientation is changed
(c) decrease if it is taken partially out of the liquid
(d) be in the vertically upward direction.
An ornament weighing 36 g in air, weighs only 34 g in water. Assuming that some copper is mixed with gold to prepare the ornament, find the amount of copper in it. Specific gravity of gold is 19.3 and that of copper is 8.9.
Refer to the previous problem. Suppose, the goldsmith argues that he has not mixed copper or any other material with gold, rather some cavities might have been left inside the ornament. Calculate the volume of the cavities left that will allow the weights given in that problem.
A cylindrical object of outer diameter 20 cm and mass 2 kg floats in water with its axis vertical. If it is slightly depressed and then released, find the time period of the resulting simple harmonic motion of the object.
A cube of ice of edge 4 cm is placed in an empty cylindrical glass of inner diameter 6 cm. Assume that the ice melts uniformly from each side so that it always retains its cubical shape. Remembering that ice is lighter than water, find the length of the edge of the ice cube at the instant it just leaves contact with the bottom of the glass.
A motor boat having a length of 10 m and a breadth of 5 cm is floating on a lake. The boat sinks by 5 cm when the load gets on it. What is the mass of the load?
A wooden block with a coin placed on its top, floats in water as shown in figure. The distance l and h are shown in the figure. After some time the coin falls into the water. Then ______.
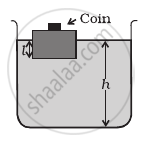
- l decreases.
- h decreases.
- l increases.
- h increase.
