Advertisements
Advertisements
Question
A first-order reaction takes 69.3 min for 50% completion. What is the time needed for 80% of the reaction to get completed? (Given: log 5 = 0.6990, log 8 = 0.9030, log 2 = 0.3010)
Solution
Half-life `t_(1/2) = 0.693/k`
k = `0.693/69.3 = 1/100` = 0.01 min–1
For first-order reaction
k = `2.303/t log ([Ro])/([R])`
t = `2.303/0.01 log 100/20`
t = 230.3 log 5 (log 5 = 0.6990)
t = 160.9 min
APPEARS IN
RELATED QUESTIONS
Sucrose decomposes in acid solution to give glucose and fructose according to the first order rate law. The half life of the reaction is 3 hours. Calculate fraction of sucrose which will remain after 8 hours.
During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1μg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
The rate constant for the first order decomposition of H2O2 is given by the following equation:
log k = 14.34 − 1.25 × 104 K/T. Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
The half-life period of zero order reaction A → product is given by
(a) `([A]_0)/k`
(b) `0.693/k`
(c) `[A]_0/(2k)`
(d) `(2[A]_0)/k`
After 2 hours, a radioactive substance becomes `(1/16)^"th"` of original amount. Then the half life ( in min) is
Define half life of a reaction.
Calculate half-life period of life order reaction whose rate constant is 200 sec–1
Observe the graph shown in figure and answer the following questions:
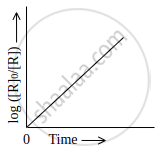
Write the relationship between k and t1/2 (half-life period)
For the given first order reaction A → B the half life of the reaction is 0.3010 min. The ratio of the initial concentration of reactant to the concentration of reactant at time 2.0 min will be equal to ______. (Nearest integer)
Assertion (A): The half-life of a reaction is the time in which the concentration of the reactant is reduced to one-half of its initial concentration.
Reason (R): In first-order kinetics, when the concentration of reactant is doubled, its half-life is doubled.
