Advertisements
Advertisements
Question
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
Solution
Given,
The focal length of the concave mirror is f and M is the mass of the gun. Horizontal speed of the bullet is V.
Let the recoil speed of the gun be Vg
Using the conservation of linear momentum we can write,
`MV_g = mV`
⇒ `V_g = m/M `V
Considering the position of gun and bullet at time t = t,
For the mirror, object distance, u = − (Vt + Vgt)
Focal length, f = − f
Image distance, v = ?
Using Mirror formula, we have:
`1/v + 1/u = 1/f`
⇒ `1/v + 1/u = 1/f `
⇒ `1/v = 1/-f - 1/u`
⇒ `1/v = -1/f + 1/ ( Vt + V_ g t)`
⇒ `1/v = (-(Vt + V_g t) + f)/( (Vt + V_g t) f`
⇒ `v = (-(Vt - V _g t ) tf) / ( f - (V + Vg) t)`
The separation between image of the bullet and bullet at time t is given by:
`v = u -(( V + V_g )tf )/ ( f- ( V + V g) t + ( V + Vg ) t`
`= (V + Vg ) t [ f/ (f-(V + Vg )t) + 1]`
`= 2( 1 + m/M )Vt`
Differentiating the above equation with respect to 't' we get,
`d ( v -u ) = 2 ( 1 + m/M ) V`
Therefore, the speed of separation of the bullet and image just after the gun was fired is
`2 ( 1 + m/M ) V`.
APPEARS IN
RELATED QUESTIONS
A mobile phone lies along the principal axis of a concave mirror. Show, with the help of a suitable diagram, the formation of its image. Explain why magnification is not uniform.
A convex lens of focal length 20 cm is placed coaxially with a concave mirror of focal length 10 cm at a distance of 50 cm apart from each other. A beam of light coming parallel to the principal axis is incident on the convex lens. Find the position of the final image formed by this combination. Draw the ray diagram showing the formation of the image
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept 15 cm apart. A point object is placed 40 cm in front of the convex lens. Find the position of the image formed by this combination. Draw the ray diagram showing the image formation.
A convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
An object AB is kept in front of a concave mirror as shown in the figure.
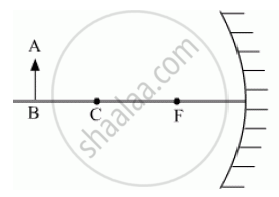
(i) Complete the ray diagram showing the image formation of the object.
(ii) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black?
Use Huygens’ geometrical construction to show the behavior of a plane wavefront.
(i) Passing through a biconvex lens;
(ii) Reflecting by a concave mirror
Find the diameter of the image of the moon formed by a spherical concave mirror of focal length 7.6 m. The diameter of the moon is 3450 km and the distance between the earth and the moon is 3.8 × 105 km.
A particle goes in a circle of radius 2.0 cm. A concave mirror of focal length 20 cm is placed with its principal axis passing through the centre of the circle and perpendicular to its plane. The distance between the pole of the mirror and the centre of the circle is 30 cm. Calculate the radius of the circle formed by the image.
A concave mirror of radius R is kept on a horizontal table (See figure). Water (refractive index = μ) is poured into it up to a height h. Where should an object be placed so that its image is formed on itself?

A hemispherical portion of the surface of a solid glass sphere (μ = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
The convex surface of a thin concavo-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place? (b) If the concave part is filled with water (μ = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.
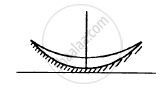
A small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t < d/V, (b) at a time t > d/V.
A mass m = 50 g is dropped on a vertical spring of spring constant 500 N m−1 from a height h = 10 cm as shown in figure. The mass sticks to the spring and executes simple harmonic oscillations after that. A concave mirror of focal length 12 cm facing the mass is fixed with its principal axis coinciding with the line of motion of the mass, its pole being at a distance of 30 cm from the free end of the spring. Find the length in which the image of the mass oscillates.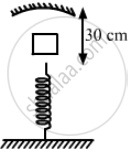
In the case of a concave mirror of focal length f , when an object is kept between f and 2 f , show that its image is formed beyond 2 f .
