Advertisements
Advertisements
Question
A half-life is the amount of time that it takes for a radioactive substance to decay to one half of its original quantity.
Suppose radioactive decay causes 300 grams of a substance to decrease to 300 × 2–3 grams after 3 half-lives. Evaluate 300 × 2–3 to determine how many grams of the substance are left.
Explain why the expression 300 × 2–n can be used to find the amount of the substance that remains after n half-lives.
Solution
Since, 300 g of a substance is decrease to 300 × 2–3 g after 3 half-lives.
So, we have to evaluate `300 xx 2^-3 = 300/8 = 37.5` g ...[∵ 23 = 8]
APPEARS IN
RELATED QUESTIONS
Express the given numbers in usual form.
1.0001 × 109
Express the following numbers in standard form:
846 × 107
Write the following numbers in the usual form:
1.0001 × 109
Write the following numbers in the usual form:
3.61492 × 106
Large numbers can be expressed in the standard form by using positive exponents.
Write 39,00,00,000 in the standard form.
The number of red blood cells per cubic millimetre of blood is approximately 5.5 million. If the average body contains 5 litres of blood, what is the total number of red cells in the body? Write the standard form. (1 litre = 1,00,000 mm3)
Express the following in standard form:
Human body has 1 trillon of cells which vary in shapes and sizes.
Express the following in standard form:
Express 56 km in m.
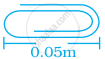
The paper clip below has the indicated length. What is the length in standard form.