Advertisements
Advertisements
Question
A heavy ring of mass m is clamped on the periphery of al light circular disc. A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre moves in a circle of radius r with a uniform speed v. We conclude that an external force
Options
\[\frac{m v^2}{r}\] must be acting on the central particle
\[\frac{2m v^2}{r}\] must be acting on the central particle
\[\frac{2m v^2}{r}\] must be acting on the system
\[\frac{2m v^2}{r}\] must be acting on the ring.
Solution
\[\frac{2m v^2}{r}\] must be acting on the system
Total mass of the system = 2m
To move the centre of the system in a circle of radius r with a uniform speed v, the external force required is
\[\frac{2m v^2}{R}\]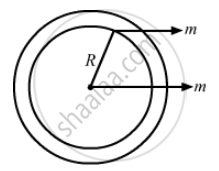
APPEARS IN
RELATED QUESTIONS
What can be said about the centre of mass of a uniform hemisphere without making any calculation? Will its distance from the centre be more than r/2 or less than r/2?
A uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre
A uniform disc of radius R is put over another uniform disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
A disc of radius R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
One end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity \[\omega\] The force exerted by the clamp on the rod has a horizontal component
A uniform rod is kept vertically on a horizontal smooth surface at a point O. If it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain _________ .
A uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to test. Assuming that the chain does not form a heap on the floor calculate the force exerted by it on the floor when a length x has reached the floor.
A square plate of mass 120 g and edge 5⋅0 cm rotates about one of the edges. If it has a uniform angular acceleration of 0⋅2 rad/s2 what torque acts on the plate?
Calculate the torque on the square plate of the previous problem if it rotates about a diagonal with the same angular acceleration.
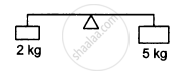
A light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the following figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.
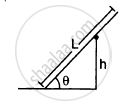
A uniform rod of length L rests against a smooth roller as shown in the following figure. Find the friction coefficient between the ground and the lower end if the minimum angle that the rod can make the horizontal is θ.
A uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate (a) the angular momentum of the rod about the axis of rotation, (b) the speed of the centre of the rod and (c) its kinetic energy.
A uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle. Show that if the mass of the rod is four times that of the particle, the collision is elastic.
