Advertisements
Advertisements
Question
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm2. What maximum pressure would the smaller piston have to bear?
Solution 1
The maximum mass of a car that can be lifted, m = 3000 kg
Area of cross-section of the load-carrying piston, A = 425 cm2 = 425 × 10–4 m2
The maximum force exerted by the load, F = mg
= 3000 × 9.8
= 29400 N
The maximum pressure exerted on the load-carrying piston, `P = F/A`
`= 29400/(425xx10^(-4))`
= 6.917 × 105 Pa
Pressure is transmitted equally in all directions in a liquid. Therefore, the maximum pressure that the smaller piston would have to bear is 6.917 × 105 Pa.
Solution 2
Pressure on the piston due to car = `"Weight of car"/"Area of piston"`
`P = (3000xx9.8)/(425xx10^(-4)) Nm^(-2) = 6.92 xx 10^5 "Pa"`
This is also the maximum pressure that the smaller piston would have to bear.
APPEARS IN
RELATED QUESTIONS
A cubical block of density ρ is floating on the surface of water. Out of its height L, fraction x is submerged in water. The vessel is in an elevator accelerating upward with acceleration a . What is the fraction immersed?
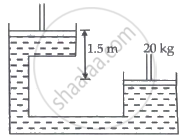
In a hydraulic press, there is a larger piston of diameter 35 cm at a height of 1.5 m relative to the smaller piston of diameter 10 cm. A 20 kg mass is loaded on the smaller piston. The density of oil in the press is 750 kg/m3. The thrust on the load by the larger piston is ______.