Question

A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?

Options

• `8/3` cm/sec

• `31/5` cm/sec

• `6/7` cm/sec

• `3/31` cm/sec

Answer 1

`8/3` cm/sec

Explanation:

Let AB be the ladder and OB be the wall

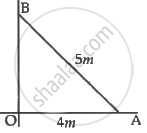
At an instant, Let OA = x, OB = y

∴ `x^2 + y^2` = 25  ......(1)

On differentiating, we get

`2x (dx)/(dt) + 2y (dy)/(dt)` = 0

⇒ `x (dx)/(dt) + y (dy)/(dt)` = 0 ......(2)

When x = 4, then from (1), we have

16 + y² = 15

⇒  y² = 9

⇒ y = 3

Now, `(dx)/(dt)` = 0.02 m/sec  .....(Given)

Putting there values in (2), we have

`4 xx 0. 0^2 + 3 (dy)/(dt)` = 0

⇒ `(dy)/(dt) = - 0.08/3 = 8/300 = - 2/75`

Hence the height of the ladder on the wall is decreasing at the rate of `2/75` m/sec = `8/3` cm/sec.