Question

A large vessel completely filled with water has two holes 'A' and 'B' at depths 'h' and '4h' from the top. Hole 'A' is a square of side 'L' and hole 'B' is circle of radius 'R'. If from both the holes same quantity of water is flowing per second, then side of square hole is ______.

Options

• 2πR

• `sqrt(2pi) * "R"`

• `"R"/2`

• `sqrt(2pi"R")`

Answer 1

A large vessel completely filled with water has two holes 'A' and 'B' at depths 'h' and '4h' from the top. Hole 'A' is a square of side 'L' and hole 'B' is circle of radius 'R'. If from both the holes same quantity of water is flowing per second, then side of square hole is `underline(sqrt(2pi) * "R")`.

Explanation:

The ratio of velocities of water is given by

`"V"_"A"/"V"_"B" = sqrt("h"/"4h") = 1/2`

`therefore "V"_"B" = 2 "V"_"A"`

Quantity of water flowing is same

∴ V_A × L² = V_B × πR²

∴ V_A L² = 2 V_A × πR²

∴ L² = 2πR² 

L = `sqrt(2pi) * "R"`

OR

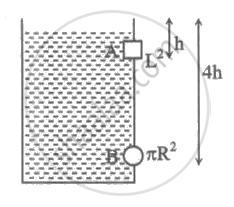
`"v"_1=sqrt(2gh)`

`"v"_2=sqrt(2g4h)`

`therefore "A"_1"v"_1="A"_2"v"_2`

`"L"^2sqrt(2gh)=pi"R"^2sqrt(2g4h)`

L² = 2πR²

`therefore"L"=sqrt(2pi)*"R"`