Advertisements
Advertisements
Question
A line segment AP stands at point P of a straight line BC such that ∠APB = 5x – 40° and ∠APC = .x+ 10°; find the value of x and angle APB.
Solution
AP stands on BC at P and
∠APB = 5x – 40°, ∠APC = x + 10°
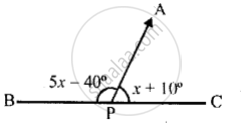
(i) ∵ APE is a straight line
∠APB + ∠APC = 180°
⇒ 5x – 40° + x + 10° = 180°
⇒ 6x - 30°= 180°
⇒ 6x = 180° + 30° = 210°
x = `210^circ/6` = 35°
(ii) and ∠APB = 5x – 40° = 5 x 35° – 40°
= 175 ° – 40° = 135°
APPEARS IN
RELATED QUESTIONS
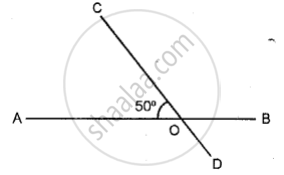
Two straight lines AB and CD intersect each other at a point O and angle AOC = 50° ; find:
(i) angle BOD
(ii) ∠AOD
(iii) ∠BOC
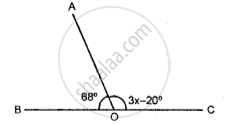
The given diagram, shows two adjacent angles AOB and AOC, whose exterior sides are along the same straight line. Find the value of x
The figure given below shows a pair of adjacent angles AOB and BOC. Find whether or not the exterior arms OA and OC are in the same straight line
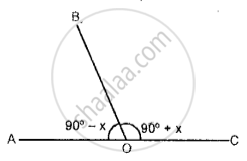
The figure given below shows a pair of adjacent angles AOB and BOC. Find whether or not the exterior arms OA and OC are in the same straight line

Identify the pair of angles in the figure given below :
adjacent angles, vertically opposite angles, interior alternate angles, corresponding angles or exterior alternate angles.
- ∠2 and ∠4
- ∠1 and ∠8
- ∠4 and ∠5
- ∠1 and ∠5
- ∠3 and ∠5
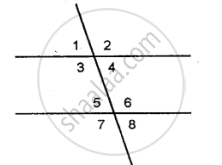
Identify the pair of angles in the figure given below :
adjacent angles, vertically opposite angles, interior alternate angles, corresponding angles or exterior alternate angles.
- ∠2 and ∠7
- ∠4 and ∠8
- ∠1 and ∠8
- ∠1 and ∠5
- ∠4 and ∠7
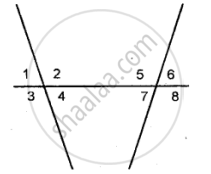
Identify the pair of angles in the figure given below :
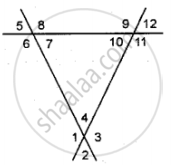
adjacent angles, vertically opposite angles, interior alternate angles, corresponding angles or exterior alternate angles.
- ∠1 and ∠10
- ∠6 and ∠12
- ∠8 and ∠10
- ∠4 and ∠11
- ∠2 and ∠8
- ∠5 and ∠7
In the case, given below, draw perpendicular to AB from an exterior point P.
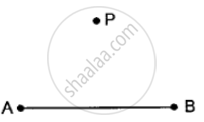
In the case, given below, draw perpendicular to AB from an exterior point P.
Draw a line segment BC = 8 cm. Using set-squares, draw ∠CBA = 60° and ∠BCA = 75°. Measure the angle BAC. Also measure the lengths of AB and AC.
