Question

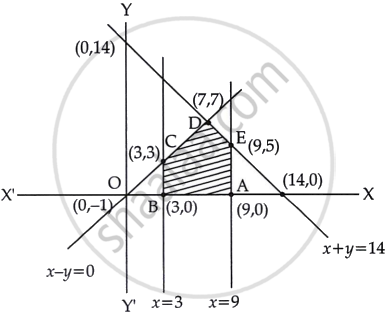
A Linear Programming Problem is as follows:

Minimise                           z = 2x + y

Subject to the constraints x ≥ 3, x ≤ 9, y ≥ 0
                                          x – y ≥ 0, x + y ≤ 14

The feasible region has 

Options

• 5 corner points including (0, 0) and (9, 5)

• 5 corner points including (7, 7) and (3, 3)

• 5 corner points including (14, 0) and (9, 0)

• 5 corner points including (3, 6) and (9, 5)

Answer 1

5 corner points including (7, 7) and (3, 3)

Explanation:

On plotting the constraints x = 3, x = 9, x = y and x + y = 14, we get the following graph. From the graph given below it clear that feasible region is ABCDEA, including corner points A(9, 0), B(3, 0), C(3, 3), D(7, 7) and E(9, 5).

Thus, feasible region has 5 corner points including (7, 7) and (3, 3).