Advertisements
Advertisements
Question
A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone if it is good but the trader will only buy a mobile if it has no major defect. One phone is selected at random from the lot. What is the probability that it is acceptable to the trader?
Solution
Given, total number of mobile phones
n(S) = 48
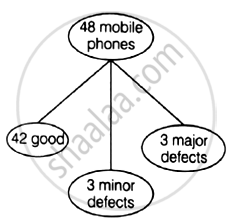
Let E2 = Event that trader will buy only when it has no major defects
= Trader will buy only 45 mobiles
∴ n(E2) = 45
∴ `P(E_2) = (n(E_2))/(n(S)) = 45/48 = 15/16`
APPEARS IN
RELATED QUESTIONS
The probability of an event that is certain to happen is ______. Such as event is called ______.
A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that she will buy it?
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is Red
From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is a king of black color.
A box contains 150 bulbs out of which 15 are defective. It is not possible to just look at a bulb and tell whether or not it is defective. One bulb is taken out at random from this box. Calculate the probability that the bulb taken out is a good one.
1000 families with 2 children were selected randomly , and the following data were recorded :
| Number of girls in a family | 0 | 1 | 2 |
| Number of families | 333 | 392 | 275 |
Find the probability of a family , having
(i) 1 girl
In a cricket match a batsman hits a boundary 6 times out of 30 balls he plays. Find the probability that he did not hit the boundary?
The chance of throwing 5 with an ordinary die is ____________.
A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a green ball.
There is a square board of side ‘2a’ units circumscribing a red circle. Jayadev is asked to keep a dot on the above said board. The probability that he keeps the dot on the shaded region is ______.