Question

A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore

Answer 1

Let AB be the cliff and C and D be the two positions of th fishing trawler.

Then, ∠ACB = 30º and ∠ADB = 60º

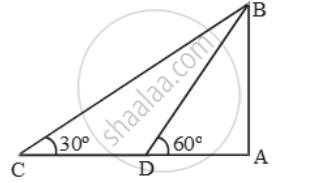
Let AB = h.

`\text{Now, }\frac{AD}{AB}=\text{cot }60^\text{o}=\frac{1}{\sqrt{3}}`

`\Rightarrow AD=\frac{h}{\sqrt{3}}`

`\text{And, }\frac{AC}{AB}=\text{cot 3}0^\text{o}=\sqrt{3}`

⇒ AC = √3 h

`CD=ACAD=( \sqrt{3}h-\frac{h}{\sqrt{3}})=\frac{2h}{\sqrt{3}}`

Let u m/min be the uniform speed of the trawler.

Distance covered in 6 min = 6u metres.

`\therefore CD=6u\Rightarrow \frac{2h}{\sqrt{3}}=6u\Rightarrowh=3\sqrt{3}u`

`Now,\text{ }AD=\frac{h}{\sqrt{3}}=\frac{3\sqrt{3}u}{\sqrt{3}}=3u`

Time taken by trawler to reach A

`=>\frac{`