Advertisements
Advertisements
Question
A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the (horizontal) distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building? (take g = 10 m/s2)
Solution
Horizontal Projectile: When a body is projected horizontally from a certain height ‘y’ vertically above the ground with initial velocity u. If friction is considered to be absent, then there is no other horizontal force which can affect the horizontal motion. The horizontal velocity therefore remains constant and so the object covers an equal distance in the horizontal direction in equal intervals of time.
Time of flight: If a body is projected horizontally from a height h with velocity u and the time taken by the body to reach the ground is T, then
`h = 0 + 1/2 gT^2` ......(For vertical motion)
`T = sqrt((2h)/g)`
Horizontal range: Let R be the horizontal distance travelled by the body
`R = uT + 1/2 0T^2` .......(For horizontal motion a = 0)
`R = u sqrt((2h)/g)`
We will apply kinematic one by one downward and horizontal. We first consider motion horizontal and there is no horizontal force which can affect horizontal motion. The horizontal velocity therefore remains constant and so the object covers an equal distance in the horizontal direction in equal intervals of time.
According to the problem, the horizontal speed of the man (ux) = 9 m/s Horizontal distance between the two buildings = 10 m
Height difference between the two buildings = 9 m and g = 10 m/s2
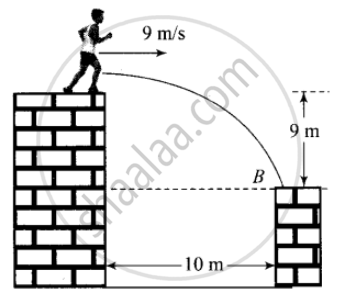
Let the man jumps from point A and land on the roof of the next building at point B.
Taking motion in the vertical direction,
`y = ut + 1/2 at^2`
9 = `0 xx t + 1/2 xx 10 xx t^2`
9 = 5t2
or t = `sqrt(9/5) = 3/sqrt(5)`
∴ Horizontal distance travelled = `u_x xx t = 9 xx 3/sqrt(5) = 27/sqrt(5)` m ≈ 12 m
The horizontal distance travelled by the man is greater than 10 m, therefore, he will land on the next building.
APPEARS IN
RELATED QUESTIONS
Two projectiles A and B are projected with angle of projection 15° for the projectile A and 45° for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
A particle moves along the X-axis as x = u (t − 2 s) + a (t − 2 s)2.
(a) the initial velocity of the particle is u
(b) the acceleration of the particle is a
(c) the acceleration of the particle is 2a
(d) at t = 2 s particle is at the origin.
A man has to go 50 m due north, 40 m due east and 20 m due south to reach a field. (a) What distance he has to walk to reach the field? (b) What is his displacement from his house to the field?
A particle starts from the origin, goes along the X-axis to the point (20 m, 0) and then return along the same line to the point (−20 m, 0). Find the distance and displacement of the particle during the trip.
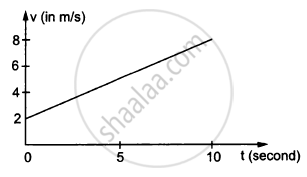
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the distance travelled in 0 to 10s
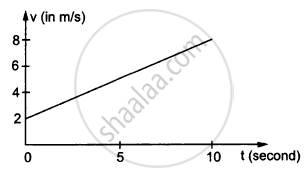
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the displacement in 0 to 10 s.
A ball is dropped and its displacement vs time graph is as shown figure (displacement x is from ground and all quantities are +ve upwards).

- Plot qualitatively velocity vs time graph.
- Plot qualitatively acceleration vs time graph.
The velocity-displacement graph of a particle is shown in figure.
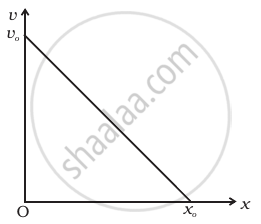
- Write the relation between v and x.
- Obtain the relation between acceleration and displacement and plot it.
Ship A is sailing towards the northeast with velocity `vecv = 30hati + 50hatj` km/hr where `hati` points east and `hatj`, north. Ship B is at a distance of 80 km east and 150 km north of Ship A and is sailing west at 10 km/hr. A will be at the minimum distance from B in ______.
A car covers the first half of the distance between two places at 40 km/h and other half at 60 km/h. The average speed of the car is ______.
