Question

A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?

Answer 1

Let VAB be the solid metallic right circular cone of height 20 cm. suppose this cone is cut by a plane parallel to its base of a point O' such that VO' = O'O i.e O' is the mid-point of VO. 

Let r₁ and r₂ be the radii of circular ends of the frustum ABB'A'

 

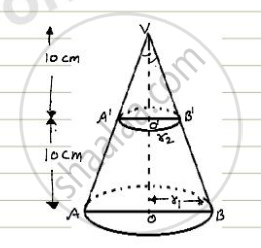
In triangle VOA we have

 tan 45° = `(OA)/(VO)`

 `rArr1=r_1/20`

`rArr r_1 = 20  cm`

Now, in Δ VO'A' we have 

tan`45^@=(O'A')/(VO')`

`rArr 1= r_2/10`

`rArr r_2 = 10  cm`

∴ volume of the frustum 

`=1/3pi(r_1^2+r_2^2+r_1r_2)h`

Volume of the frustum

`(pi)/3(20^2+10^2+20xx10)xx20`

`=(pi)/3(400+100+200)xx10`

`=700(pi)/3  cm^3`

 Let the length of the wire of 1/16 cm

diameter be l cm. then,

radius of wire = 1/32 cm

Volume of the metal used in wire `= (pil)/1024 cm^2`

Since the frustum is recast into a wire of lenght l cm and diameter 1/16 cm.

∴ Volume of the metal used in wire = Volume of the frustum

`rArr (pil)/1024 = 7000(pi)/3`

`rArr l/1024=7000/3`

`rArr l= 700/3xx1024`

= 2389333.33 cm

= 23893.33 m

Hence, the lenght of wire is 23893.33 m.