Advertisements
Advertisements
Question
A motor car slows down from 72 kmh−1 to 36 kmh−1 over a distance of 25 m. If the brakes are applied with the same force
calculate
- total time in which car comes to rest
- distance travelled by it.
Solution

Take motion of a car from A to B:
u = 72 kmh−1 = `72xx5/18` ms−1
u = 20 ms−1
v = 36 kmh−1 = `36xx5/18` ms−1
v = 10 ms−1
(Time) t1 = ?
Acceleration = a = ?
Distance = S1 = 25 m
v2 − u2 = 2aS1
(10)2 − (20)2 = 2a (25)
50a = 100 − 400 = −300
a = `-300/50` = −6 ms−2
Now, v = u + at1
10 = 20 + (−6) t1
6t1 = 20 − 10 = 10
t1 = `10/6` = 1.67s
Take motion of a car from B to C:
u = 36 kmh−1 = 10 ms−1
v = 0
a = −6 ms−2
(Time) t2 = ?
(Distance) S2 = ?
v = u + at2
0 = 10 + (−6) t2
6t2 = 10
t2 = `10/6` = 1.67S
Now, v2 − u2 = 2aS2
(0)2 − (10)2 = 2 (−6) S2
−12S2 = −100
S2 = `100/12` = 8.33 m
Total time taken by car from A to C = t1 + t2 = `10/6+10/6`
= `(10+10)/6=20/6` = 3.33s
Total distance covered by car from A to C = S1 + S2
= 25 + 8.33 = 33.33 m
APPEARS IN
RELATED QUESTIONS
What can you say about the nature of motion of a body if its displacement-time graph is A straight line inclined to the time axis with an acute angle?
A body starts with an initial velocity of 10m s-1 and acceleration 5 m s-2. Find the distance covered by it in 5 s.
The figure represents graphically the velocity of a car moving along a straight road over a period of 100 hours.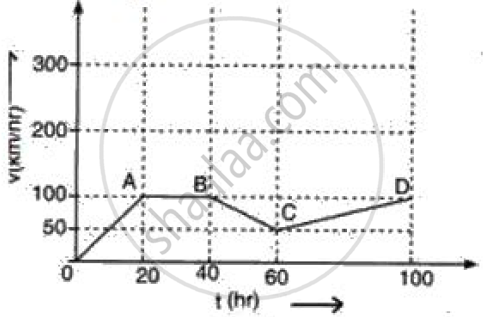
Calculate the distance travelled in the last 40 h.
An object covers a distance of S meters in t seconds as follows :
| S (meters) | 0 | 8 | 20 | 20 | 16 | 10 | 0 |
| t (Seconds) | 80 | 2 | 5 | 10 | 12 | 15 | 10 |
Plot a graph, taking t on X-axis and S on Y-axis. Determine the velocity of the object at time
(i) 6 s, and
(ii) 14 s.
State whether true or false. If false, correct the statement.
Distance covered by a particle never becomes zero but displacement becomes zero.
______ is the length of the actual path covered by a body.
Write a note on the following:
knot
An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height of 100 m. What is the difference in their heights after 2s if both the objects drop with the same accelerations? How does the difference in heights vary with time?
A particle is moving in a circular pattern of radius r. The displacement after half a circle would be ______.
A body is projected up with an initial velocity of u m/s. It goes up to a height, ‘h’ meters in seconds' time. Then it comes back at the point of projection.
Considering negligible air resistance, which of the following statement is true?
