Advertisements
Advertisements
Question
A multistorey building has 25 floors above the ground level each of height 5 m. It also has 3 floors in the basement each of height 5 m. A lift in building moves at a rate of 1 m/s. If a man starts from 5 0m above the ground, how long will it take him to reach at 2nd floor of basement?
Solution
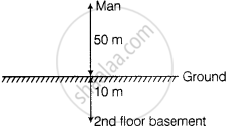
Man covers the distance above the ground = 50 m
And man covers the distance below the ground = 2 × 5 = 10 m ......[∵ Distance between two floors = 5 m]
Thus, total distance = 50 m + 10 m = 60 m
∵ Speed of the lift = 1 m/s ......[Given]
Hence, time taken to reach second floor of basement = `"Distance"/"Speed"`
= `(60 m)/(1 m/s)`
= 60 s or 1 min
APPEARS IN
RELATED QUESTIONS
Find the product, using suitable properties:
26 × (− 48) + (− 48) × (− 36)
Find the product, using suitable properties:
625 × (− 35) + (− 625) × 65
In a class test containing 10 questions, 5 marks are awarded for every correct answer and (− 2) marks are awarded for every incorrect answer and 0 for questions not attempted.
Mohan gets four correct and six incorrect answers. What is his score?
Find the following products: (– 18) × (– 10) × 9
Find the following products: (– 20) × (– 2) × (– 5) × 7
Find (– 23) × 48
Find 52 × (– 8) + (–52) × 2
If * is an operation have, such that for integers a and b. We have a * b = a × b + (a × a + b × b), then find (–3) * (–5)
If * is an operation have, such that for integers a and b. We have a * b = a × b + (a × a + b × b), then find (–6) * 2
The given table shows the freezing points in °F of different gases at sea level. Convert each of these into °C to the nearest integral value using the relation and complete the table,
C = `5/9 (F - 32)`
| Gas | Freezing Point at Sea Level (°F) |
Freezing Point at Sea Level (°C) |
| Hydrogen | –435 | |
| Krypton | –251 | |
| Oxygen | –369 | |
| Helium | –458 | |
| Argon | –309 |
