Advertisements
Advertisements
Question
A normal eye has retina 2 cm behind the eye-lens. What is the power of the eye-lens when the eye is (a) fully relaxed, (b) most strained?
Solution
(a) When the eye lens is fully relaxed, we have:
u = ∞
Distance of the retina from the eye lens, v = 2 cm = 0.02 m
The lens formula is given by
`1/v -1/u =1/f`
Putting the respective values, we get:
`1/f = 1/0.02 - 1/∞ = 1/0.02`
∴ Power of the lens =`1/f` = 50 diopters
So, in a fully relaxed condition, the power of the eye lens is 50 D.
(b) When the eye lens is most strained:
u = – 25 cm = – 0.25 m
The lens formula is given by
`1/v -1/u =1/f`
Putting the values, we get:
`1/f = 1/0.02 -1/((-0.25))`
= 50+4 =54
∴ Power of the lens = `1/f` = 54 diopters
So, in the most strained condition, the power of the eye lens is 54 D.
APPEARS IN
RELATED QUESTIONS
A virtual image, we always say, cannot be caught on a screen. Yet when we ‘see’ a virtual image, we are obviously bringing it on to the ‘screen’ (i.e., the retina) of our eye. Is there a contradiction?
Does short-sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodation? If not, what might cause these defects of vision?
A myopic person has been using spectacles of power −1.0 dioptre for distant vision. During old age, he also needs to use the separate reading glass of power + 2.0 dioptres. Explain what may have happened.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to? How is such a defect of vision corrected?
The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?
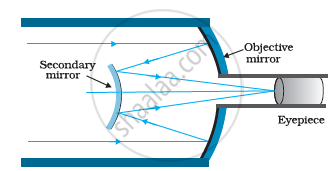
A Cassegrain telescope uses two mirrors as shown in the figure. Such a telescope is built with the mirrors 20 mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?
A person A can clearly see objects between 25 cm and 200 cm. Which of the following may represent the range of clear vision for a person B having muscles stronger than A, but all other parameters of eye identical to that of A?
The focal length of a normal eye-lens is about
The distance of the eye-lens from the retina is x. For a normal eye, the maximum focal length of the eye-lens
A man wearing glasses of focal length +1 m cannot clearly see beyond 1 m
When we see an object, the image formed on the retina is
(a) real
(b) virtual
(c) erect
(d) inverted
Mark the correct options.
(a) If the far point goes ahead, the power of the divergent lens should be reduced.
(b) If the near point goes ahead, the power of the convergent lens should be reduced.
(c) If the far point is 1 m away from the eye, divergent lens should be used.
(d) If the near point is 1 m away from the eye, divergent lens should be used.
A nearsighted person cannot see beyond 25 cm. Assuming that the separation of the glass from the eye is 1 cm, find the power of lens needed to see distant objects.
A myopic adult has a far point at 0.1 m. His power of accomodation is 4 diopters.
- What power lenses are required to see distant objects?
- What is his near point without glasses?
- What is his near point with glasses? (Take the image distance from the lens of the eye to the retina to be 2 cm.)
