Question

A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by² as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?

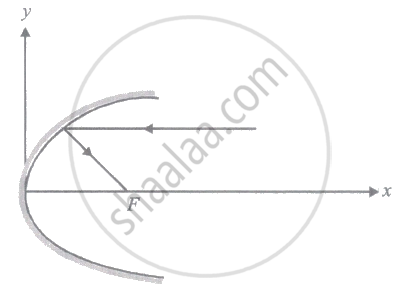
Options

• `1/"2b"`

• `1/"8b"`

• `1/"4b"`

• `1/"b"`

Answer 1

`1/"8b"`

Explanation:

Let the ray is incident at a point P = (x₁, y₁) on the mirror. Then slope at P,

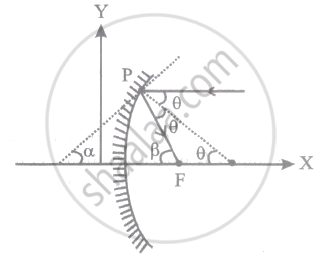
`tan(alpha) = ("dy"/"dt")_((x_1),"y"_1) = 1/(4("b"))`    ...(I)

(α) = 90° - (θ) and (β) = 2(θ)

Now, the reflected ray is passing through P(x₁, y₁) and has slope tan (β). Hence, then equation will be

`("y" - "y"_1)/(x - x_1) = - (tan beta) = (- tan 2theta) = (- 2 tan theta)/(1 - tan^2 theta)`

`therefore ("y" - "y"_1) = (2 cot (alpha))/(1 + cot(alpha)) (x_1 - (x))`      ...(ii)

Further, (x₁) = 4(by₁)²     ...(iii)

At F, x = 0     ...(iv)

From eq. (i) to eq. (iv), we get x = `1/"8b"`

It shows that the coordinates of F are unique `(1/"8b", 0)`.

Hence, the reflected ray passing through one focus and the focal length = `1/(8"b")`.