Advertisements
Advertisements
Question
A path 5 m wide runs along the inside of the rectangular field. The length of the rectangular field is three times the breadth of the field. If the area of the path is 500 m2 then find the length and breadth of the field
Advertisements
Solution
Let the length of the rectangular field = ‘L’ m
Breadth of the rectangular field = ‘B’ m
Area of the rectangular field = (L × B) m2
Also given length = 3 × Breadth
L = 3B
Width of the path (W) = 5 m
Lenth of the inner rectangle = L – 2W
= l – 2(5)
= 3B – 10 m
Breadth of the inner rectangle = B – 2W
= B – 2(5)
= B – 10 m
Area of the inner rectangle = (3B – 10)(B – 10)
= 3B2 – 10B – 30B + 100
Area of the path = Area of outer rectangle – Area of inner rectangle
= (L × B) – (3B2 – 10B – 30B + 100)
= 3B × B – (3B2 – 40B + 100)
= 3B2 – 3B2 + 40B – 100
Area of the path = 40B – 100
Given area of the path = 500 m2
40B – 100 = 500
40B = 500 + 100 = 600
B = `600/40`
B = 15 m
Length of the field = 45 m, Breadth of the field = 15 m
APPEARS IN
RELATED QUESTIONS
A circular carpet whose radius is 106 cm is laid on a circular hall of radius 120 cm. Find the area of the hall uncovered by the carpet
A school ground is in the shape of a circle with radius 103 m. Four tracks each of 3 m wide has to be constructed inside the ground for the purpose of track events. Find the cost of constructing the track at the rate of ₹ 50 per sq.m
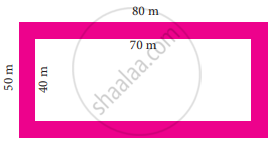
A picture is painted on a ceiling of a marriage hall whose length and breadth are 18 m and 7 m respectively. There is a border of 10 cm along each of its sides. Find the area of the border
The formula used to find the area of the rectangular path is
The formula to find the width of the circular path is
Four circles are drawn side by side in a line and enclosed by a rectangle as shown below. If the radius of each of the circles is 3 cm, then calculate:
(i) The area of the rectangle.
(ii) The area of each circle.
(iii) The shaded area inside the rectangle.
A circular path has to be constructed around a circular lawn. If the outer and inner circumferences of the path are 88 cm and 44 cm respectively, find the width and area of the path
A goat is tethered with a rope of length 45 m at the centre of the circular grassland whose radius is 52 m. Find the area of the grassland that the goat cannot graze
A strip of 4 cm wide is cut and removed from all the sides of the rectangular cardboard with dimensions 30 cm × 20 cm. Find the area of the removed portion and area of the remaining cardboard
A rectangular field is of dimension 20 m × 15 m. Two paths run parallel to the sides of the rectangle through the centre of the field. The width of the longer path is 2 m and that of the shorter path is 1 m. Find (i) the area of the paths (ii) the area of the remaining portion of the field (iii) the cost of constructing the roads at the rate of ₹ 10 per sq.m
