Advertisements
Advertisements
Question
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
Solution
In this case, acceleration is variable. In accelerated motion, the weight of body depends on the magnitude and direction of acceleration for upward or downward motion.

a. Hence, the weight of the body changes during oscillations
b. Considering the situation in two extreme positions. as their acceleration is maximum in magnitude.
We have, mg – N = ma
∵ At the highest point, the platform is accelerating downward.
⇒ N = mg – ma
But a = ω2A .....[In magnitude]
∴ N = mg – mω2A
Where, A = amplitude of motion
Given, m = 50 kg, frequency v = 2 s–1
∴ ω = 2πv = 4π rad/s
A = 5 cm = 5 × 10–2 m
∴ N = 50 × 9.8 – 50 × (4π)2 × 5×10–2
= 50[9.8 – 16π2 × 5 × 10–2]
= 50[9.8 – 7.89]
= 50 × 1.91
= 95.5 N
When the platform is at the lowest position of its oscillation,
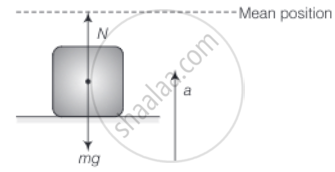
It is accelerating towards the mean position that is vertically upwards.
Writing the equation of motion
N – mg = ma = mω2A
or N = mg + mω2A
= m[g + ω2A]
Putting the data N = 50[9.8 + (4π)2 × 5 × 10–2]
= 50[9.8 + (12.56)2 × 5 × 10–2]
= 50[9.8 + 7.88]
= 50 × 17.68
= 884 N
Now, the machine reads the normal reaction. It is clear that
Maximum weight = 884 N ......(At lowest point)
Minimum weight = 955 N .....(At top point)
