Advertisements
Advertisements
Question
A person starts his trip from home. He moves 24 km in south direction and then starts moving towards east. He travels 7 km in that direction and finally reaches his destination. How far is the destination from his home?
Solution
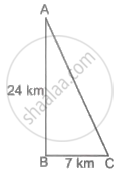
Let A represent his home, AB represent the distance to the south, and BC represent the distance to the east.
Thus, distance between his destination and his home is AC.
According to the Pythagoras theorem,
AB2 + BC2 = AC2
Putting values for AB and BC in equation (i),
242 + 72 = AC2
576 + 49 = AC2
AC2 = 625
AC = `sqrt(625)` = 25
As a result, it is 25 kilometres between his home and his destination.
APPEARS IN
RELATED QUESTIONS
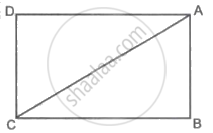
In the above figure `square`ABCD is a rectangle. If AB = 5, AC = 13, then complete the following activity to find BC.
Activity: ΔABC is a `square` triangle.
∴ By Pythagoras theorem
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
Construct two concentric circles with centre O with radii 3 cm and 5 cm. Construct a tangent to a smaller circle from any point A on the larger circle. Measure and write the length of the tangent segment. Calculate the length of the tangent segment using Pythagoras' theorem.
In the right-angled triangle ABC, Hypotenuse AC = 10 and side AB = 5, then what is the measure of ∠A?
If tan θ = `12/5`, then 5 sin θ – 12 cos θ = ?
From the information in the figure, complete the following activity to find the length of the hypotenuse AC.

AB = BC = `square`
∴ ∠BAC = `square`
Side opposite angle 45° = `square/square` × Hypotenuse
∴ `5sqrt(2) = 1/square` × AC
∴ AC = `5sqrt(2) xx square = square`
AB, BC and AC are three sides of a right-angled triangle having lengths 6 cm, 8 cm and 10 cm, respectively. To verify the Pythagoras theorem for this triangle, fill in the boxes:
ΔABC is a right-angled triangle and ∠ABC = 90°.
So, by the Pythagoras theorem,
`square` + `square` = `square`
Substituting 6 cm for AB and 8 cm for BC in L.H.S.
`square` + `square` = `square` + `square`
= `square` + `square`
= `square`
Substituting 10 cm for AC in R.H.S.
`square` = `square`
= `square`
Since, L.H.S. = R.H.S.
Hence, the Pythagoras theorem is verified.
There is a ladder of length 32 m which rests on a pole. If the height of pole is 18 m, determine the distance between the foot of ladder and the pole.
Find the side of a square whose diagonal is `10sqrt2` cm.
