Advertisements
Advertisements
Question
A pitcher with 1-mm thick porous walls contains 10 kg of water. Water comes to its outer surface and evaporates at the rate of 0.1 g s−1. The surface area of the pitcher (one side) = 200 cm2. The room temperature = 42°C, latent heat of vaporization = 2.27 × 106 J kg−1, and the thermal conductivity of the porous walls = 0.80 J s−1 m−1°C−1. Calculate the temperature of water in the pitcher when it attains a constant value.
Solution
Thickness of porous walls, l = 1mm = 10-3 m
mass, m =10 kg
Latent heat of vapourisation, Lv = 2.27 × 106 J/kg
Thermal conductivity, K = 0.80 J/m s °C
ΔQ = 2.27 × 106 × 10 J
0.1 g of water evaporate in 1 sec, so 10 kg water will evaporate in 105 s
`⇒ (DeltaQ)/(Deltat) = (2.27 xx 107)/10^5`
`⇒ (DeltaQ)/(Deltat) = 2.27 xx 10^2 ` J/s
`⇒ (DeltaQ)/(Deltat)=(DeltaT)/(l/(kA))`
`⇒ (DeltaQ)/( Deltat) = ((42 - T)/ 10^-3) . 0.80 xx 2 xx 10^-2`
⇒ `2.27xx10^2=(42-"T")/10^-3xx0.80xx2xx10^-2`
⇒ T = 27.8° C
⇒ T = 28° C
APPEARS IN
RELATED QUESTIONS
A brick weighing 4.0 kg is dropped into a 1.0 m deep river from a height of 2.0 m. Assuming that 80% of the gravitational potential energy is finally converted into thermal energy, find this thermal energy is calorie.
A van of mass 1500 kg travelling at a speed of 54 km h−1 is stopped in 10 s. Assuming that all the mechanical energy lost appears as thermal energy in the brake mechanism, find the average rate of production of thermal energy is cal s−1.
The blocks of masses 10 kg and 20 kg moving at speeds of 10 m s−1 and 20 m s−1respectively in opposite directions, approach each other and collide. If the collision is completely inelastic, find the thermal energy developed in the process.
The thermal conductivity of a rod depends on
A hot liquid is kept in a big room. The logarithm of the numerical value of the temperature difference between the liquid and the room is plotted against time. The plot will be very nearly
The ends of a metre stick are maintained at 100°C and 0°C. One end of a rod is maintained at 25°C. Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
Three rods of lengths 20 cm each and area of cross section 1 cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB = 50 J s−1 m−1°C−1, KBC = 200 J s−1m−1°C−1 and KAC = 400 J s−1 m−1°C−1. The junctions A, B and C are maintained at 40°C, 80°C and 80°C respectively. Find the rate of heat flowing through the rods AB, AC and BC.
A metal rod of cross sectional area 1.0 cm2 is being heated at one end. At one time, the temperatures gradient is 5.0°C cm−1 at cross section A and is 2.5°C cm−1 at cross section B. Calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB = 0.40 J°C−1, thermal conductivity of the material of the rod = 200 W m−1°C−1. Neglect any loss of heat to the atmosphere
A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2. The inner surface (a cylinder a length d and radius r1) is maintained at a temperature θ1 and the outer surface (a cylinder of length d and radius r2) is maintained at a temperature θ2 (θ1 > θ2). The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.
A hollow tube has a length l, inner radius R1 and outer radius R2. The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2 (T2 > T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2.
Figure (28-E2) shows a copper rod joined to a steel rod. The rods have equal length and equal cross sectional area. The free end of the copper rod is kept at 0°C and that of the steel rod is kept at 100°C. Find the temperature at the junction of the rods. Conductivity of copper = 390 W m−1°C−1 and that if steel = 46 W m−1°C−1.

Following Figure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20 cm and area of cross section 0.20 cm2. The junction is maintained at a constant temperature 40°C and the two ends are maintained at 80°C. Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivites are KAt = 200 W m−1°C−1 and KCu = 400 W m−1°C−1.

Suppose the bent part of the frame of the previous problem has a thermal conductivity of 780 J s−1 m−1 °C−1 whereas it is 390 J s−1 m−1°C−1 for the straight part. Calculate the ratio of the rate of heat flow through the bent part to the rate of heat flow through the straight part.
The two rods shown in following figure have identical geometrical dimensions. They are in contact with two heat baths at temperatures 100°C and 0°C. The temperature of the junction is 70°C. Find the temperature of the junction if the rods are interchanged.

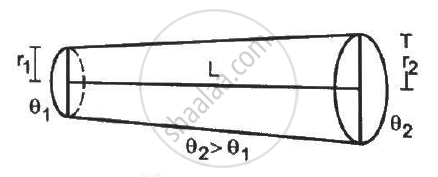
Find the rate of heat flow through a cross section of the rod shown in figure (28-E10) (θ2 > θ1). Thermal conductivity of the material of the rod is K.
A hollow metallic sphere of radius 20 cm surrounds a concentric metallic sphere of radius 5 cm. The space between the two spheres is filled with a nonmetallic material. The inner and outer spheres are maintained at 50°C and 10°C respectively and it is found that 100 J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the spheres.
