Question

A pole 6m high is fixed on the top of a tower. The angle of elevation of the top of the pole observed from a point P on the ground is 60° and the angle of depression of the point P from the top of the tower is 45°. Find the height of the tower and the distance of point P from the foot of the tower. (Use `sqrt3` = 1.73)

Answer 1

Consider QR as the tower, PQ as the pole on it. Given, ∠PAR = 60° and ∠QAR = 45°

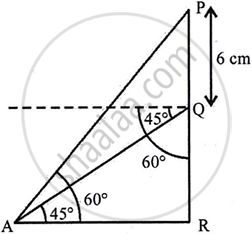
Let QR = hm   

Since PQ = 6m   (given)

∴ PR = 6 + h   ...(i)

In right ΔQAR,

`tan45^circ = (QR)/(AR)`

⇒ `1 = h/(AR)`

⇒ AR = hm     ...(ii)

In right ΔPAR,

`tan60^circ = (PR)/(AR)`

⇒ `sqrt3 = (6 + h)/h`       ...[From eq. (i) and (ii)]

⇒ `sqrt3h = 6 + h`

⇒ `h = 6/(sqrt3 - 1)`

⇒ `h = 6/((1.732 - 1))`

⇒ `h = 6/0.732 = 6000/732 = 8.196`

⇒ h = 8.20m

Height of tower, QR = h = 8.20m

Distance of point P from the foot of the tower

= PR = 6 + h 

= 6 + 8.20

= 14.20m