Question

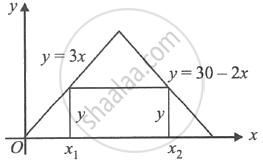
A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is ______.

Options

• `135/8`

• 45

• `135/2`

• 90

Answer 1

A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is `underlinebb(135/2)`.

Explanation:

A = (x₂ – x₁)y

y = 3x₁ and y = 30 – 2x₂

A(y) = `((30 - y)/2 - y/3)y`

6A(y) = (90 – 3y – 2y)y = 90y – 5y²

6A'(y) = 90 – 10y = 0

`\implies` y = 9; A"(y) = –10 < 0

x₁ = 3; x₂ = `21/2`

`\implies` A_max = `(21/2 - 3)9 = (15 xx 9)/2 = 135/2`