Question

A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is ______.

Options

• 15°

• 30°

• 60°

• 75°

Answer 1

A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is 60°.

Explanation:

We have AC = secθ, AG = 8

∴ CG = 8 – secθ (C being the peg).

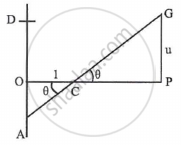
But u = CG sin θ = (8 – secθ) sinθ

u = 8 sin θ – tanθ

`(du)/(dθ)` = 8 cos θ – sec² θ,

`(d^2u)/(dθ^2)` = –8 sin θ – 2 sec² θ tan θ

`(du)/(dθ)` = 0, when cos³θ = `1/8`, cos θ = `1/2`,

`(d^2u)/(dθ^2)` > 0 (atθ = 60°), ∴ θ = 60°