Question

A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses `(m/M)` is `1/x`. The value of 'x' will be ______.

Options

• 1

• 2

• 3

• 4

Answer 1

A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses `(m/M)` is `1/x`. The value of 'x' will be 4.

Explanation:

Conservation of linear momentum

mu = Mv

Therefore, v = mu/M .............(i)

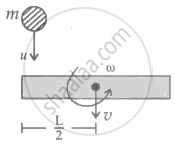
Conservation of angular momentum,

`"mu" L/2 = Iω`

`"mu" L/2 = (ML^2)/12ω`

or, ω = `(6"mu")/(ML)` ...........(ii)

As, e = 1 for the coefficient of restitution for a perfectly elastic collision.

⇒ `e = (V_2 - V_1)/(u_1 - u_2) = ((v + omegaL/Z) - 0)/(u - 0)`

1 = `(v + (omegaL)/2)/u`

u = `v + (omegaL)/2`

The result of equations (i), (ii), and (iii) is as follows:

`u = ("mu")/M + (3"mu")/M = (4"mu")/M`

`m/M = 1/4`

so, x = 4