Question

A simple pendulum with a bob of mass m and conducting wire of length L swings under gravity through an angle θ. The component of the earth's magnetic field in the direction perpendicular to the swing is B. Maximum emf induced across the pendulum is ______.

(g = acceleration due to gravity)

 

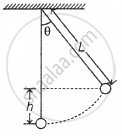
Options

• `BL sin(theta/2)(gL)`

• `2BLsin(theta/2)(gL)^{3"/"2}`

• `2BLsin(theta/2)(gL)^2`

• `2BLsin(theta/2)(gL)^{1"/"2}`

Answer 1

A simple pendulum with a bob of mass m and conducting wire of length L swings under gravity through an angle θ. The component of the earth's magnetic field in the direction perpendicular to the swing is B. Maximum emf induced across the pendulum is `underlinebb(2BLsin(theta/2)(gL)^{1"/"2})`.

Explanation:

When the bob reaches point B from point A as shown below, then the vertical height travelled by the bob,

h = L - L cosθ

⇒ h = L(1 - cosθ)

 

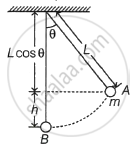
The velocity of the bob at point B is v and at A is u, which is zero at the extreme point, i.e. u = 0 then from the equation,

v² = u² + 2gh

∴ v² = 2gh = 2gL(1 - cosθ) = 2gL(2sin²θ/2) [∵ 1 - cosθ = 2sin²`theta/2`]

⇒ v = `2sqrt(gL)sin  theta/2`

Thus, maximum emf induced,

`e_{max} = B"v"L = B xx 2sqrt(gL)(sin  theta"/"2)L`

= 2BL(sinθ/2)(gL)^1/2