Question

A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.

Answer 1

 

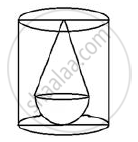
Radius of cylinder = 3 cm
Height of cylinder = 6 cm
Radius of hemisphere = 2 cm
Height of cone = 4 cm
Volume of water in the cylinder when it is full = 

`pir^2h=pixx3xx3xx6=54picm^3` 

Volume of water displaced = volume of cone + volume of
hemisphere 

`=1/3pir^2h+2/3pir^3` 

`=1/3pir^2(h+2r)` 

`=1/3pixx2xx2(4+2xx2)` 

`=1/3pixx4xx8` 

`=32/3picm^3` 

Therefore, volume of water which is left 

`=54pi-32/3pi` 

`=130/3picm^3` 

`=130/3xx22/7cm^3` 

`2860/21cm^3` 

`=136.19cm^3` 

`=136cm^3`