Question

A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:

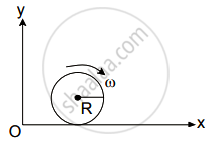
Options

• 2

• 3

• 5

• 4

Answer 1

5

Explanation:

Given: Mass of hollow sphere = 1 kg

Radius of sphere = R

When a sphere is rolling only, it will be rotating about its centre of mass with an angular speed of w and performing translatory motion at the same time with velocity = v_cm Condition for pure rolling, v_cm = Rω

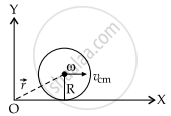
⇒ Total Angular momentum of Rolling Sphere = Angular momentum due to rotation about it's centre of mass + Moment of linear momentum possessed by centre of mass about origin.

⇒ L_net = L_cm + `vec"r" xx ("M"vec"v"_("cm"))`

⇒ L_net = Iω + Mv_cm × r_⊥ar

⇒ L_net = Iω + Mv_cmR

Where r_⊥ar is the perpendicular distance between centre of mass and line passing from origin

∴ r_⊥ar = R

Moment of inertia of hollow sphere about its centre of mass = `2/3` MR²

L_o = `2/3` MR² ω² + 1 × Rω × R

L_o = `2/3` × 1 × R²ω × R²ω

L_o = R²ω `[2/3+1]`

L_o = `5/3`  R²ω

So, by comparing it with given value, we get, a = 5