Advertisements
Advertisements
Question
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
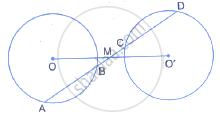
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
Solution
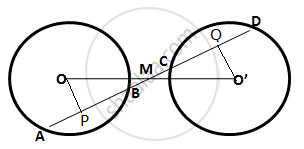
Given: A straight line Ad intersects two circles of equal radii at A, B, C and D.
The line joining the centres O O' intersect AD at M
And M is the midpoint of OO'.
To prove: AB = CD
Construction: From O, draw OP⊥AB and from O’, draw O 'Q⊥CD.
Proof:
In ΔOMP and Δ O' MQ,
∠OMP = ∠O'MQ (vertically opposite angles)
∠OPM = ∠O'QM (each = 90°)
OM = O'M (Given)
By Angle – Angle – Side criterion of congruence,
∴ ΔOMP ≅ O'MQ, (by AAS)
The corresponding parts of the congruent triangle are congruent
∴ OP = O'Q (c.p.ct)
We know that two chords of a circle or equal circles which are equidistant from the centre are equal.
∴ AB = CD
