Advertisements
Advertisements
Question
A student wants to project the image of a candle flame on a screen 60 cm in front of a mirror by keeping the flame at a distance of 15 cm from its pole.
(a) Write the type of mirror he should use.
(b) Find the linear magnification of the image produced.
(c) What is the distance between the object and its image?
(d) Draw a ray diagram to show the image formation in this case.
Solution
(a) He should use a concave mirror, as it forms a real image on the same side of the mirror.
(b) Object distance, u = -15 cm
Image distance, v = - 60 cm
`"Magnification, "m=-v/u=-((-60))/((-15))=-4" cm"`
The minus sign in magnification shows that the image formed is real and inverted.
(c) The image is formed at a distance of 45 cm from the object.
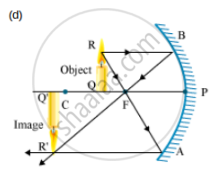
In this case, the image is formed beyond the centre of curvature. This image is real, inverted and enlarged.
APPEARS IN
RELATED QUESTIONS
A divergent lens of focal length 30 cm forms the image of an object of size 6 cm on the same side as the object at a distance of 15 cm from its optical centre. Use lens formula to determine the distance of the object from the lens and the size of the image formed.
An object of height 4 cm is placed at a distance of 20 cm from a concave lens of focal length 10 cm. Use lens formula to determine the position of the image formed.
Magnification produced by a convex mirror is always:
(a) more than 1
(b) less than 1
(c) equal to 1
(d) more or less than 1
In order to obtain a magnification of −2 (minus 2) with a concave mirror, the object should be placed:
(a) between pole and focus
(b) between focus and centre of curvature
(c) at the centre of curvature
(d) beyond the centre of curvature
A concave mirror produces magnification of +4. The object is placed:
(a) at the focus
(b) between focus and centre of curvature
(c) between focus and pole
(d) between the centre of curvature
In order to obtain a magnification of, −1.5 with a concave mirror of focal length 16 cm, the object will have to be placed at a distance
(a) between 6 cm and 16 cm
(b) between 32 cm and 16 cm
(c) between 48 cm and 32 cm
(d) beyond 64 cm
The lens A produces a magnification of, − 0.6 whereas lens B produces a magnification of + 0.6.
What is the nature of lens B?
At what distance should an object be placed from a lens of focal length 25 cm to obtain its image on a screen placed on the other side at a distance of 50 cm from the lens? What will be the magnification produced in this case?
Give scientific reason.
Simple microscope is used for watch repairs.
Solve the following example.
An object kept 60 cm from a lens gives a virtual image 20 cm in front of the lens. What is the focal length of the lens? Is it a converging lens or diverging lens?
