Question

A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ₀r with ρ₀ as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR². The value of the coefficient a is ______.

Options

• `1/2`

• `3/5`

• `8/5`

• `3/2`

Answer 1

A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ₀r with ρ₀ as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR². The value of the coefficient a is `underlinebb(8/5)`.

Explanation:

Given:

A circular plate of mass M and radius R has a density that varies as ρ(r) = ρ₀r, where ρ₀ is a constant and r is the distance from the centre,

The moment of inertia about an axis perpendicular to the plate and passing through its edge is I = a MR².

To find: Value of coefficient a in,

I = a MR².

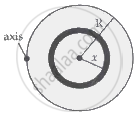
Consider a ring with a radius of x and a thickness of dx, as shown in the diagram above. This ring will have the following moment of inertia about an axis that is perpendicular to the plate and passes through its centre:

dI_xc = dm × x² = ρ₀ x(2πx dx) × x²

= 2πρ₀ x⁴ dx ........(i)

This ring's moment of inertia about an axis perpendicular to the plate and passing through its edge is:

dI_x = dmx² + dmR²

= `2pirho_0x^4  dx + rho_0x(2pix  dx)R^2`

= `2pirho_0x^4 dx + 2pirho_0x^2R^2dx` .........(ii)

The entire plate's moment of inertia about an axis that passes through its edge and is perpendicular to the plate will be:

`I = intdI_x`

= `int_0^R (2pirho_0x^4)dx + int_0^R 2pirho_0x^2R^2 dx`

I = `(2pirho_0[x^5]_0^R)/5 + (2pirho_0R^2[x^3]_0^R)/3`

I = `16/15pirho_0R^5` .........(iii)

Mass of the ring:

M = ∫dm

= `intrho_0x(2pix dx)`

= `2pirho_0int_0^Rx^2 dx = 2/3pirho_0R^3` .....(iv)

Equation (iii) can also be written as:

I = `8/5 xx (2/3 pirho_0R^3)R^2`

= `8/5MR^2` .......(v)

On comparing equation (v) with I = aMR², we get:

a = `8/5`