Question

A thin metal wire of length 'L' and uniform linear mass density 'ρ' is bent into a circular coil with 'O' as centre. The moment of inertia of a coil about the axis XX' is ______.

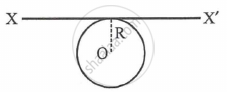
Options

• `(3rho "L"^3)/(8pi^2)`

• `(rho "L"^3)/(4pi^2)`

• `(3rho "L"^2)/(4pi^2)`

• `(rho "L"^3)/(8pi^2)`

Answer 1

A thin metal wire of length 'L' and uniform linear mass density 'ρ' is bent into a circular coil with 'O' as centre. The moment of inertia of a coil about the axis XX' is `underlinebb((3rho "L"^3)/(8pi^2))`.

Explanation:

Moment of inertia of a thin circular coil,

I = `"MR"^2/2`

Now, moment of inertia of a ring about axis XX' as in figure below,

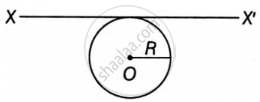
`"I"_"xx" = "MR"^2/2 + "MR"^2`

`= 3/2 "MR"^2`    ...(i)   (Using theorem of parallel axis)

Given, L = length of wire of ring

and ρ = linear mass density

Then, mass of the ring = linear density × length

⇒ M = ρL    ...(ii)

and L = 2πR

⇒ R = `"L"/(2pi)`      ....(iii)

Now, putting the value from Eqs. (ii) and (iii) in (i), we get

`"I"_"xx" = 3/2 (rho"L") "L"^2/(4pi^2) = (3rho"L"^3)/(8pi^2)`