Question

A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.

Options

• 30 m

• 20 m

• 45 m

• 35 m

Answer 1

20 m

Explanation:

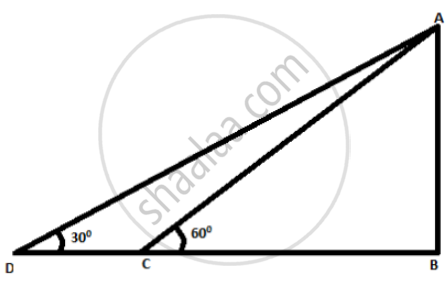
Applying the function 'tan' in ∆ABC

`"tan" ("C") = "AB"/"BC"`

`=> "tan"  (60) = (10 sqrt3 "m")/"BC"`

`=> sqrt3 = (10 sqrt3 "m")/"BC"`

`=> "BC" = (10 sqrt3)/sqrt3`

`=> "BC" = 10 "m"`

And applying in the ∆ABD we have

`"tan" ("D") = "AB"/"BD"`

`"tan"  30 = (10 sqrt3 "m")/"BD"`

`=> 1/sqrt3 = (10 sqrt3 "m")/"BD"`

`=> "BD" = 10 xx 3 "m"`

`=> "BD" = 30 "m"`

Now the distance between the opposite bank of the canal and the point with a 30° angle of elevation is CD:

BD - BC

= 30 m - 10 m

= 20 m