Advertisements
Advertisements
Question
A uniform magnetic field B(t), pointing upward fills a circular region of radius, s in a horizontal plane. If B is changing with time, find the induced electric field.
Solution
The area of the region, A= πs2, remains constant, while B = B(t) is a function of time. Therefore, the induced electric field,
e = `- ("d" phi)/"dt"`
= `- "d"/"dt" (vec "B" * vec"A")`
= `- A (dB(t))/(dt)`
= `- pis^2 (dB(t))/(dt)`
Note: The volt and volt per metre are the SI units for the two physical quantities, emf and electric field, respectively. As a result, the question has been updated.
APPEARS IN
RELATED QUESTIONS
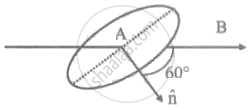
A coil of area A = 0.8 m2 is situated in a uniform magnetic field B = 6.0 Wb/m2 and makes an angle of 60° with respect to the magnetic field as shown in figure. The value of the magnetic flux through the area A would be equal to ______.
A small loop of area of cross-section 10-6 m2 is lying concentrically and coplanar inside a bigger loop of radius 0.628 m. A current of 20 A is passed in the bigger loop. The smaller loop is rotated about its diameter with an angular velocity `omega`. The magnetic flux linked with the smaller loop will be ____________.
A rectangular loop of area 0.4 m2 is lying in a magnetic field of 4 x 10-2 tesla at an angle of 60° with the magnetic field. The magnetic flux passing through this loop will be ______.
