Question

A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.

Options

• `("h tan"  alpha)/("tan"  beta + "tan"  alpha)`

• `("h tan"  alpha)/("tan"  beta - "tan"  alpha)`

• `("h tan"  beta)/("tan"  beta + "tan"  alpha)`

• `("h tan"  beta)/("tan"  beta - "tan"  alpha)`

Answer 1

A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is `underline(("h tan"  alpha)/("tan"  beta - "tan"  alpha))`.

Explanation:

Observe the figure,

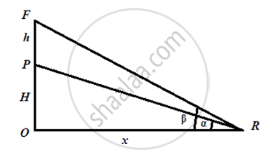
`"tan" alpha = "H"/"x"`

`=> "x" = "H"/("tan" alpha)`

Also,

`"tan" beta = ("h + H")/"x"`

`=> "x" = ("h + H")/("tan" beta)`

therefore,

`"H"/("tan" alpha) = ("h + H")/("tan" beta)`

`=> "H tan"  beta = "h tan"  alpha + "H tan"  alpha`

`=> "H tan"  beta - "H tan"  alpha = "h tan"  alpha`

`=> "H" = ("h tan"  alpha)/(("tan"  beta  - "tan"  alpha))`