Question

A vessel at rest explodes into three pieces. Two pieces having equal masses fly-off perpendicular to one another with the same velocity 30 meter per second. The third piece has three times mass of each of other piece. The magnitude and direction of the velocity of the third piece will be

Options

• `10sqrt(2)` m/second and 135° from either

• `10sqrt(2)` m/second and 45° from either

• `10/sqrt(2)` m/second and 135° from either

• `10/sqrt(2)` m/second and 45° from either

Answer 1

`10sqrt(2)` m/second and 135° from either

Explanation:

Assume that two pieces have the same mass m and a third piece has a mass of 3 m.

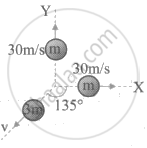
Because the system's beginning momentum was zero, the system's ultimate momentum must also be zero, according to the law of conservation of linear momentum. That is, the sum of the momentums of the first two pieces must match the momentum of the third item.

If two particles have the same momentum and the angle between them is 90°, the result is given by

p`sqrt(2)` = mv `sqrt(2)` = 30`sqrt(2)` m

Let the velocity of mass 3 m be v.

So, 3 mv = 30 m `sqrt(2)`

∴ v = `10sqrt(2)` m/s and angle 135° from either