Question

A water barrel stands on a table of height 'h'. A small hole is made on the wall of barrel at its bottom. If the stream of water coming out of the hole strikes the ground at horizontal distance 'R' from the table, the depth 'd' of water in the barrel is ______.

Options

• `h/(4R^2)`

• `R^2/(2h)`

• `R^2/(4h)`

• `(4h)/R^2`

Answer 1

A water barrel stands on a table of height 'h'. A small hole is made on the wall of barrel at its bottom. If the stream of water coming out of the hole strikes the ground at horizontal distance 'R' from the table, the depth 'd' of water in the barrel is `underline(R^2/(4h))`.

Explanation:

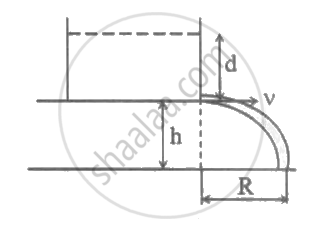
R = v

`t=sqrt(2gd)  t`

`h=1/2g t^2`

`therefore t=sqrt((2h)/g)`

`thereforeR^2=2gd xx t^2=2gd xx (2h)/g`

`d=R^2/(4h)`