Question

A wheel of radius 2 cm is at rest on the horizontal surface. A point P on the circumference of the wheel is in contact with the horizontal surface. When the wheel rolls without slipping on the surface, the displacement of point P after half rotation of wheel is ______.

Options

• `2(pi^2+2)^(1/2)`cm

• `(pi^2+2)^(1/2)`cm

• `(pi^2+4)^(1/2)`cm

• `2(pi^2+4)^(1/2)`cm

Answer 1

A wheel of radius 2 cm is at rest on the horizontal surface. A point P on the circumference of the wheel is in contact with the horizontal surface. When the wheel rolls without slipping on the surface, the displacement of point P after half rotation of wheel is `underline(2(pi^2+4)^(1/2) "cm")`.

Explanation:

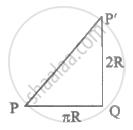
After half the rotation. the horizontal distance travelled by point P will be half the circumference of the wheel i.e. πR and the vertical distance will be 2R.

`therefore "Displacement" PP^'=sqrt(pi^2R^2+4R^2)=Rsqrt(pi^2+4)`

`=2sqrt(pi^2+4)  "cm"`