Question

A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.

Options

• h (1 - tan A cot B)

• h (1 + tan A cot B)

• `"h"/((1 - "tan A cot B"))`

• `"h"/((1 + "tan A cot B"))`

Answer 1

A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is h (1 + tan A cot B).

Explanation:

Let the height of another house be H m and the distance between two houses is x m.

From figure,

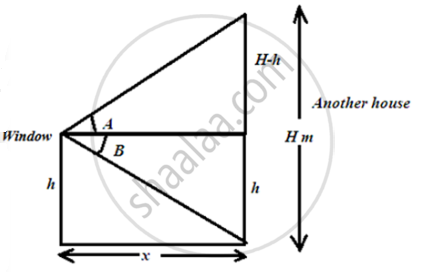
`"tan B" = "h"/"x"`

`=> "x" = "h"/("tan B")`

`"tan A" = ("H" - "h")/"x"`

`=> "x" = ("H" - "h")/("tan A")`

This implies,

`("H" - "h")/("tan A") = "h"/("tan B")`

`=> "H tan B" - "h tan B" = "h tan A"`

`=> "H tan B" = "h tan A" + "h tan B"`

`=> "H" = "h" ("tan A")/("tan B") + "h"`

`=> "H" = "h tan A cot B" + "h"`

`=> "H" = "h" ("tan A cot B" + 1)`