Question

A wire of length L is hanging from a fixed support. The length changes to L₁ and L₂ when masses 1 kg and 2 kg are suspended respectively from its free end. Then the value of L is equal to :

Options

• `sqrt("L"_1  "L"_2)`

• `("L"_1 +"L"_2)/2`

• 2 L₁ - L₂

• 3L₁ - 2L₂

Answer 1

2 L₁ - L₂

Explanation:

Given: The final length of the wire is L₁ when a mass of 1 kg is attached to it, and L₂ when a load of 2 kg is attached to it.

Let the Young’s modulus of wire material be Y, Then

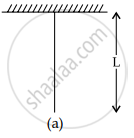
By Hooke’s Law of elasticity ⇒ `"F"/"A" = "Y"(Δl)/l`

Let area of cross-section of wire be A 

original length of wire = L

Case - I → When 1 kg load is attached to wire change in length = L₁ – L

Using Hooke’s Law

F₁ = mg = 1 × g ⇒ `(1 xx"g")/"A" = "Y" (("L"_1 - "L")/"L")`   ...(1)

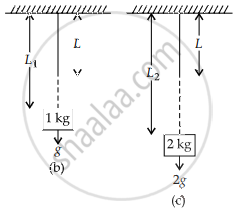
Length of wire

(a) in normal condition

(b) When 1 kg mass is suspended

(c) When 2 kg mass is suspended

Case - II → When 2 kg load is attached to wire change in length = L₂ – L

Using Hooke’s Law

F₂ = mg = 2 × g

⇒  `(2 xx"g")/"A" = "Y" (("L"_2 - "L")/"L")`    ...(2)

Dividing equation (1) by (2)

`1/2 = ("L"_1 - "L")/("L"_2 - "L")`

L₂ - L = 2L₁ - 2L

L = 2L₁ - L₂