Question

आरेखों की सहायता से सामान्य तथा विषम वितरणों में माध्य, माध्यिका तथा बहुलक की सापेक्षिक स्थितियों की व्याख्या कीजिए।

Answer 1

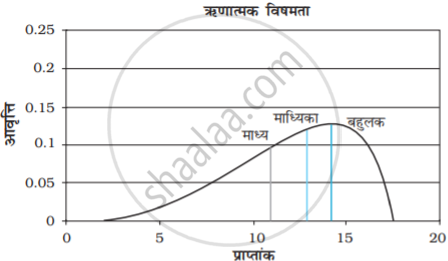
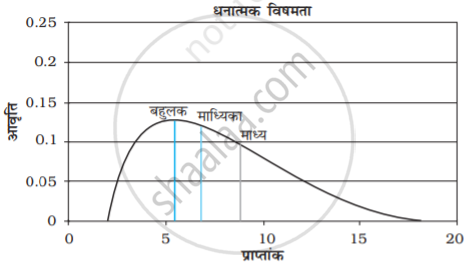
सामान्य वितरण की विशेषता है कि इसमें माध्य, माध्यिका तथा बहुलक का मान समान होता है क्योंकि सामान्य वितरण सममित होता है। इसमें अधिकतम आवृत्ति का मान, वितरण के मध्य में होता है तथा इस बिंदू से आधी इकाईयाँ ऊपर व आधी नीचे होती हैं। अति उच्च तथा अति निम्न मूल्यों की बारंबारता बहुत ही कम होती हैं। देखें चित्र सामान्य वक्र आवृत्तियों को प्रदर्शित करने वाला रेखाचित्र घंटाकार वक्र कहलाता है। सामान्य वक्र में आंकड़ों की परिवर्तनशीलता कम अथवा अधिक हो सकती है। सामान्य वक्र का एक उदाहरण है-चित्र A में धनात्मक विषमता वाला वक्र दिखाया गया है जिसमें निम्न मूल्यों की आवृत्तियाँ अधिक तथा अधिक मूल्य की आवृत्तियाँ कम है। इस स्थिति में पहले बहुलक, फिर माध्यिका तथा अंत में माध्य आता है। जबकि चित्र B में ऋणात्मक विषमता वाला वक्र दिखाया गया है। इसमें कम मूल्य की आवृत्तियाँ कम तथा अधिक मूल्य की आवृत्तियाँ अधिक होती हैं। इस स्थिति में पहले माध्य, फिर माध्यिका तथा अंत में बहुलक आता है।

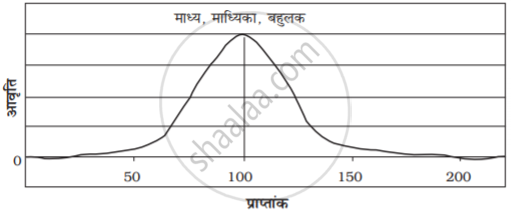
यदि आंकड़े विषम अथवा विकृत हों तो माध्य, माध्यिका तथा बहुलक संपाती नहीं होंगे। विषम आंकड़ों के प्रभाव को A तथा B के द्वारा स्पष्ट रूप से समझा जा सकता है।