Question

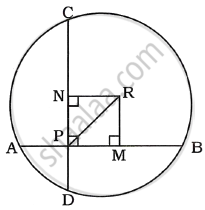
AB and CD are two chords of a circle intersecting at right angles to each other at P. If R is the centre of the circle, prove that:

`bar(PA) + bar(PB) + bar(PC) + bar(PD) = 2bar(PR)`

Answer 1

Let `bara, barb, barc, bard, barp` and `barr` be the position vectors of the points A, B, C, D, P and R respectively.

Let M and N be the midpoints of chords AB and CD respectively.

∴ The p.v. of M = `barm = (bara + barb)/2`   ...(1)

The p.v. of N = `barn = (barc + bard)/2`    ...(2)

RMPN is a rectangle.

∴ `bar(RM) = bar(NP)`

`\implies barm - barr = barp - barn`

From (1) and (2)

`bara + barb = 2barm`,

`barc + bard = 2barn`   ...(3)

Now, 

L.H.S. = `bar(PA) + bar(PB) + bar(PC) + bar(PD)`

= `(bara - barp) + (barb - barp) + (barc - barp) + (bard - barp)`

= `(bara + barb) + (barc + bard) - 4barp`

= `2barm + 2barn - 4barp`   ...[From (3)]

= `2(barm + barn - 2barp)`

= `2(barr + barp - 2barp)`

= `2(barr - barp)`

= `2bar(PR)`

= R.H.S.