Question

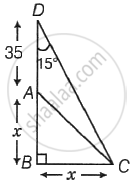
ΔABC is a right angled isosceles triangle with ∠B = 90°. If D is a point on AB, ∠CDB = 15° and AD = 35 cm, then CD is equal to ______.

Options

• `35sqrt(2)` cm

• `70sqrt(2)` cm

• `(35sqrt(3))/2` cm

• `35sqrt(6)` cm

Answer 1

ΔABC is a right angled isosceles triangle with ∠B = 90°. If D is a point on AB, ∠CDB = 15° and AD = 35 cm, then CD is equal to `underlinebb(35sqrt(2)  cm)`.

Explanation:

In ΔBCD, tan 15° = `(BC)/(BD) \implies (1 - 1/sqrt(3))/(1 + 1/sqrt(3)) = x/(x + 35)`

`\implies (sqrt(3) - 1)/(sqrt(3) + 1) = x/(x + 35)`

`\implies sqrt(3)x + 35sqrt(3) - x - 35 = sqrt(3)x + x`

`\implies` x = `(35(sqrt(3) - 1))/2`

Now, CD = `sqrt((35/2)^2 {(sqrt(3) + 1)^2 + (sqrt(3) - 1)^2}`

= `35/2 xx 2sqrt(2)`

= `35sqrt(2)` cm