Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
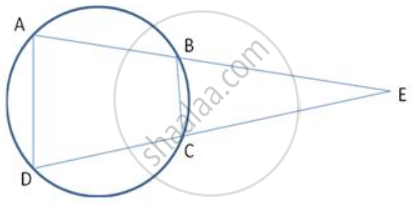
Sum
Solution
In cyclic quadrilateral ABCD ,
∠BAD + ∠ BCD = 180° - (1)
Opposite angles of cyclic quadrilateral
Also , ∠ BCD + ∠ BCE = 180° - (2) (Linear pair)
From (1) and (2) , we get
∠BAD = ∠BCE
In Δ EBC and Δ EDA
∠BAD = ∠BCE (proved above)
∠ BEC = ∠ DEA (common)
∴ Δ EBC ~ Δ EDA (AA corollary)
shaalaa.com
Is there an error in this question or solution?
