Question

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______ 

Options

• 35°

• 85°

• 90°

• 115°

Answer 1

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is 115°.

Explanation:

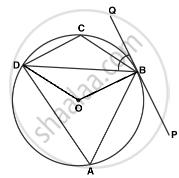
Join OB and OD

We know that OB is perpendicular to PQ.

∠OBD = ∠OBQ - ∠DBQ

∠OBD = 90° - 65°

∠OBD = 25°

OB = OD (radius)

∠OBD = ∠ODB = 25°

In △ODB

∠OBD + ∠ODB + ∠BOD = 180°

25° + 25° + ∠BOD = 180°

∠BOD = 130°

∠BAD = `1/2`∠BOD

(Angle subtended by a chord on the centre is double the angle subtended on the circle)

∠BAD = `1/2`(130°)

∠BAD = 65°

ABCD is a cyclic quadrilateral.

∠BCD + ∠BAD = 180°

∠BCD + 65° = 180°

∠BCD = 115°