Question

An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant

Answer 1

Let P and Q be the positions of two aeroplanes when Q is vertically below P and OP = 4000 m. Let the angles of elevation of P and Q at a point A on the ground be 60º and 45º respectively.

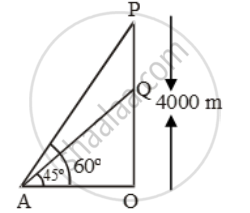
`\text{tan }60^\text{o}=\frac{OP}{OA}\text{ and tan45}^\text{o}=\frac{OQ}{OA}`

`\Rightarrow \sqrt{3}=\frac{4000}{OA}\text{ and 1=}\frac{OQ}{OA}`

`\Rightarrow OA=\frac{4000}{\sqrt{3}}\text{ and }OQ=OA`

`\Rightarrow OQ=\frac{4000}{\sqrt{3}}m`

In triangles AOP and AOQ, we have

∴ Vertical distance between the aeroplanes

= PQ = OP – OQ

`=( 4000-\frac{4000}{\sqrt{3}})=4000\frac{(\sqrt{3}-1)}{\sqrt{3}}m`

= 1690.53 m