Advertisements
Advertisements
Question
An electric bulb is hanging over a table at a height of 1 m above it. The illuminance on the table directly below the bulb is 40 lux. The illuminance at a point on the table 1 m away from the first point will be about ___________ .
Options
10 lux
14 lux
20 lux
28 lux
Solution
14 lux
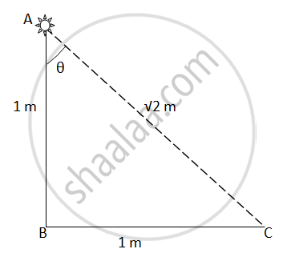
Here,
\[r = \sqrt{2}\]
\[\tan\theta = \frac{BC}{AB} = 1\]
\[ I_o = 40\text{ lux}\]
\[\theta = \tan^{- 1} \left( 1 \right) = {45}^0 \]
The illuminance is given by
\[E = \frac{I_o \cos\theta}{r^2}\]
\[ = \frac{40 \times \cos( {45}^0 )}{\left( \sqrt{2} \right)^2}\]
\[ = 14\text{ lux}\]
APPEARS IN
RELATED QUESTIONS
Light is incident normally on a small plane surface. If the surface is rotated by an angle of 30° about the incident light, does the illuminance of the surface increase, decreases or remain same? Does your answer change if the light did not fall normally on the surface?
A bulb is hanging over a table. At which portion of the table is the illuminance maximum? If a plane mirror is placed above the bulb facing the table, will the illuminance on the table increase?
The one parameter that determines the brightness of a light source sensed by an eye is ____________ .
Light from a point source falls on a screen. If the separation between the source and the screen is increased by 1%, the illuminance will decrease (nearly) by ____________ .
A battery-operated torch is adjusted to send an almost parallel beam of light. It produces an illuminancle of 40 lux when the light falls on a wall 2 m away. The illuminance produced when it falls on a wall 4 m away is close to _________ .
A point source of light moves in a straight line parallel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distance r from the source as ___________ .
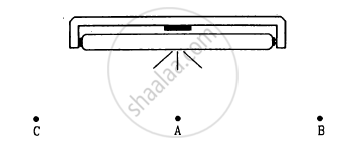
Figure shows a glowing mercury tube. The intensities at point A, B and C are related as __________ .
The brightness-producing capacity of a source
(a) does not depend on its power
(b) does not depend on the wavelength emitted
(c) depends on its power
(d) depends on the wavelength emitted
The relative luminosity of wavelength 600 nm is 0.6. Find the radiant flux of 600 nm needed to produce the same brightness sensation as produced by 120 W of radiant flux at 555 nm.
The luminous flux of a monochromatic source of 1 W is 450 lumen watt−1. Find the relative luminosity at the wavelength emitted.
A source emits light of wavelengths 555 nm and 600 nm. The radiant flux of the 555 nm part is 40 W and of the 600 nm part is 30 W. The relative luminosity at 600 nm is 0.6. Find (a) the total radiant flux, (b) the total luminous flux, (c) the luminous efficiency.
A light source emits monochromatic light of 555 nwavelengthm. The source consumes 100 W of electric power and emits 35 W of radiant flux. Calculate the overall luminous efficiency.
The illuminance of a small area changes from 900 lumen m−2 to 400 lumen m−2 when it is shifted along its normal by 10 cm. Assuming that it is illuminated by a point source placed on the normal, find the distance between the source and the area in the original position.
A point source emitting light uniformly in all directions is placed 60 cm above a table-top. The illuminance at a point on the table-top, directly below the source, is 15 lux. Find the illuminance at a point on the table-top 80 cm away from the first point.
Light from a point source falls on a small area placed perpendicular to the incident light. If the area is rotated about the incident light by an angle of 60°, by what fraction will the illuminance change?
An electric lamp and a candle produce equal illuminance at a photometer screen when they are placed at 80 cm and 20 cm from the screen respectively. The lamp is now covered with a thin paper which transmits 49% of the luminous flux. By what distance should the lamp be moved to balance the intensities at the screen again?
