Advertisements
Advertisements
Question
An electron is moving with an initial velocity `v = v_0hati` and is in a magnetic field `B = B_0hatj`. Then it’s de Broglie wavelength ______.
Options
remains constant.
increases with time.
decreases with time.
increases and decreases periodically.
Solution
An electron is moving with an initial velocity `v = v_0hati` and is in a magnetic field `B = B_0hatj`. Then it’s de Broglie wavelength remains constant.
Explanation:
If a particle is carrying a positive charge q and moving with a velocity v and enters a magnetic field 5 then it experiences a force F which is given by the expression
F = q(v × B) = $ F = qvB sin θ. As this force is perpendicular to v and B, so the magnitude of v will not change, i.e. momentum (p = mv) will remain constant in magnitude.
According to the problem, `vecv = v_0i` and `vecB = B_0j`
Magnetic force on moving electron = `-e[v_0i xx B_0j] ⇒ - ev_0B_0k`
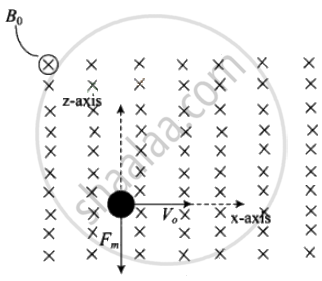
As this force is perpendicular to `vecv` and `vecB`, so the magnitude of v will not change, i.e. momentum (p = mv) will remain constant in magnitude. Hence, de-Broglie wavelength `lambda = h/(mv)` remains constant.
APPEARS IN
RELATED QUESTIONS
The wavelength of light from the spectral emission line of sodium is 589 nm. Find the kinetic energy at which
(a) an electron, and
(b) a neutron, would have the same de Broglie wavelength.
Crystal diffraction experiments can be performed using X-rays, or electrons accelerated through appropriate voltage. Which probe has greater energy? (For quantitative comparison, take the wavelength of the probe equal to 1 Å, which is of the order of inter-atomic spacing in the lattice) (me = 9.11 × 10−31 kg).
Find the typical de Broglie wavelength associated with a He atom in helium gas at room temperature (27°C) and 1 atm pressure, and compare it with the mean separation between two atoms under these conditions.
Compute the typical de Broglie wavelength of an electron in a metal at 27°C and compare it with the mean separation between two electrons in a metal which is given to be about 2 × 10−10 m.
Why photoelectric effect cannot be explained on the basis of wave nature of light? Give reasons.
A proton and α-particle are accelerated through the same potential difference. The ratio of the de-Broglie wavelength λp to that λα is _______.
An electron (mass m) with an initial velocity `v = v_0hati (v_0 > 0)` is in an electric field `E = - E_0hati `(E0 = constant > 0). It’s de Broglie wavelength at time t is given by ______.
Relativistic corrections become necessary when the expression for the kinetic energy `1/2 mv^2`, becomes comparable with mc2, where m is the mass of the particle. At what de Broglie wavelength will relativistic corrections become important for an electron?
- λ = 10 nm
- λ = 10–1 nm
- λ = 10–4 nm
- λ = 10–6 nm
The De-Broglie wavelength of electron in the third Bohr orbit of hydrogen is ______ × 10-11 m (given radius of first Bohr orbit is 5.3 × 10-11 m):
How will the de-Broglie wavelength associated with an electron be affected when the velocity of the electron decreases? Justify your answer.
