Advertisements
Advertisements
Question
An unknown planet orbits the Sun with a distance twice the semi-major axis distance of the Earth’s orbit. If the Earth’s time period is T1, what is the time period of this unknown planet?
Solution
By Kepler’s 3rd law T2 ∝ a3
Time period of unknown planet = T2
Time period of Earth = T1
Distance of unknown planet from the Sun = a2
Distance of the Earth from the Sun = a1
`"T"_1^2/"T"_2^2= "a"_1^3/"a"_2^3`
T2 = `("a"_2/"a"_1)^(3/2) "T"_1`
a2 = 2a,
T2 = `("2a"_1/"a"_1)^(3/2) "T"_1`
T2 = `2sqrt2"T"_1`
APPEARS IN
RELATED QUESTIONS
The time period of a satellite orbiting Earth in a circular orbit is independent of
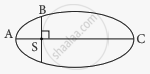
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
If a person moves from Chennai to Trichy, his weight _________.
Why is the energy of a satellite (or any other planet) negative?
What are geostationary and polar satellites?
How will you prove that Earth itself is spinning?
Derive an expression for escape speed.
Derive the time period of the satellite orbiting the Earth.
In the following, what are the quantities which that are conserved?
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle.
